How does RME do mathematics differently?
RME is about making sense of mathematics.
Realistic Mathematics Education (RME) builds deep and long-term mathematical understanding by working from contexts that make sense to students. This example of RME is taken from the American Mathematics in Context curriculum:

Mathematics teachers will recognise that this problem can be solved with simultaneous equations. Many of us trained in algebraic methods will struggle to make sense of the problem in any other way. But students who are new to algebra can quickly solve this problem without recourse to algebraic notation. Try it for yourself (start by answering the question you see, not the question you were probably expecting).
By helping students to make sense of their intuitive strategies—like visually aligning caps and umbrellas, or imagining swapping a hat for an umbrella —RME classrooms practice guided reinvention. Through this process, students gain ownership of their mathematical knowledge and a deep understanding of where mathematics comes from.
RME is about contexts, not applications.
The RME curriculum is built around contexts that have the potential to elicit powerful yet flexible mathematical models. Contexts can be taken from the real world, from fiction, or from an area of mathematics with which students are already familiar. The important thing is that students are able to imagine and engage with these scenarios.
Commonly in mathematics classrooms, students are first shown a mathematical technique and then asked to apply this technique in various settings. Images in many textbooks do little to advance students’ thinking. The image below, of a curved pitcher of orange squash, cannot help students model this recipe.

The rounded pitcher and bottle may not help students make sense of ratio.
In contrast to the problem above, the following RME questions begin by engaging students directly with the context of mixing squash. They then support students in creating their own representation of the context, from which they can build up visual ideas about ratio, while staying close to the context of mixing a drink.


While students may initially produce quite realistic drawings, the ‘straight glass’ can be increasingly stylised to support problem-solving, even when the link between context and model is less visually direct. When teachers use classroom discussion to encourage the careful observation of contexts and diagrams, students can visualise a mathematical scenario, leading to a stable model which is usable in similar contexts. These connections build confidence in thinking problems through. Students naturally develop a new willingness to try ideas out, share these ideas, and listen to others. This resilience and independence in problem solving serves them well across all areas of mathematics.
RME is about formalising, rather than formulas.
Experience shows that when students stay connected with the underlying context of a particular problem type, they are able to make sense of what they are doing, without memorising rules and procedures which have no meaning for them. Even when students move into more abstract maths—dealing with ratios, gradients or circumferences—they are able to go back to contexts that help them unpick and explain formulae.
One way of visualising the RME learning experience is through an ‘iceberg’ metaphor. While formal mathematics is visible above the water, much more lies beneath.
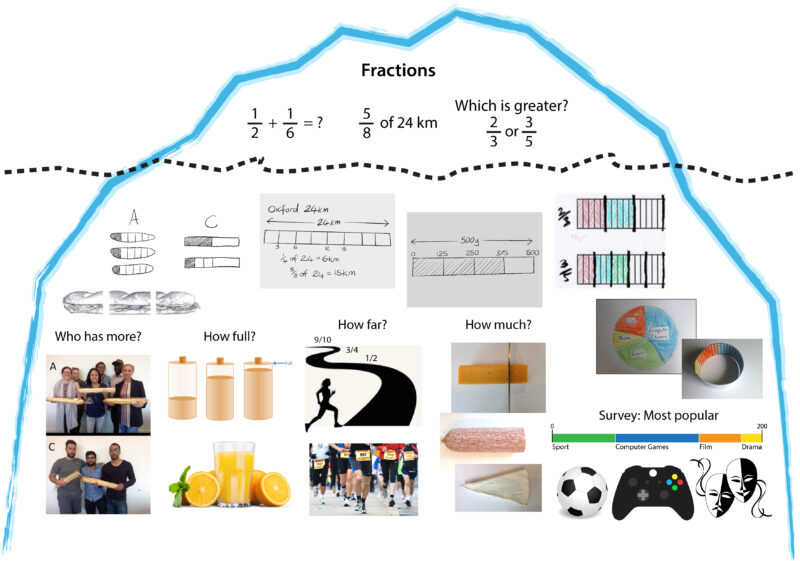
The iceberg above shows the multiple contexts that underpin an understanding of fractions in our Fair Sharing (N1) module. Without a grounding in meaningful contexts from which students can generate a number of connected representations, the formal notation of fractions could not stay afloat. In this iceberg, the subway sandwich context leads first to a representation, which is very close to the sandwich shape. This is rapidly mathematised to a bar shape. The bar appears again as a representation of distance on the stylised fun run track, and again in answer to the question ‘how much?’. Finally, we see the bar appearing as a representation of survey results, in a context which has come a long way from the subway sandwich.
When students work from meaningful contexts like these, they are doing more than learning a particular mathematical technique. By learning to examine the mathematical relationships shared across different contexts, RME pedagogy supports students in connecting their informal experiences to active and evolving ideas about the nature of fractions, working out for themselves the significance of the ‘whole’ and the need for a common denominator when comparing fractions.
RME is a process, an ethos, and an ethics.
Training in the use of RME materials helps teachers to develop a new classroom culture that features active mathematising. But, this revolution in thinking doesn’t happen overnight. Many times both pupils and instructors must work hard to develop a discussion-based classroom that can carefully evaluate new contexts and novel student strategies. Key features of an RME classroom include:
- extended discussion of multiple contexts
- development of students’ representations of contexts
- focus on multiple strategies for solving problems
- sharing, explaining and discussing strategies
Achieving these aims requires a great deal of practice and encouragement. Everyone must deepen their listening and questioning skills. And teachers must learn to facilitate “thinking time” and inter-student discussions. We have designed the “Getting Started” section of our website to provide mathematics teachers with strategies that will support this growth.
Over the long term, RME classrooms come to exhibit a class-wide commitment to learning from each other. These shifts make space for more students to contribute ideas and engage confidently in democratic, mathematical debate. They also profoundly change commonplace assumptions about what it is to do mathematics. Aligned with the creative work of mathematicians, RME exposes students to the experimental and exploratory aspects of mathematical problem solving. But, this mathematics also belongs to students’ everyday experiences and perspectives—worldviews that may not otherwise find footing in the annals of mathematical history.