RME concepts for research

On our page, What is RME, we introduced some of the key features of RME. On this page, we explore the theory behind RME further.

Several key ideas in RME have attracted us as researchers and materials designers.  All relate back to the idea of emergent mathematics. This concept is rooted in Freudenthal’s (1973, 1991) idea of “mathematics as a human activity“. His emphasis on the actions and activity of mathematical thinking, rather than on the end-product (formal mathematics), leads to a view of learning mathematics as a process of progressive mathematisation. In RME, students reinvent mathematics for themselves.

This has clear implications for the instructional design of RME materials. Classroom materials must to support reinvention by mapping out a landscape through which the classroom can travel. Materials support this progression by means of careful selection of meaningful contexts, chosen for their potential to support the generation of informal models—such as the bar or ratio table—and strategies—like re-alloting, matching,… Students arrive at conventional representations of mathematical ideas through the twin processes of horizontal and vertical mathematisation.

Emergent mathematics also has clear implications for pedagogy. It would take a very long time for students to reinvent mathematics alone. In RME, the teacher’s role is to support them in this process. Guided reinvention describes a series of techniques that enable learners to reflect on their explanations, recognise conflicts and contradictions, and consider the mathematical quality of particular strategies and models.

Context

The idea of emergent mathematics means that context plays a crucial role in the development of mathematical understanding.

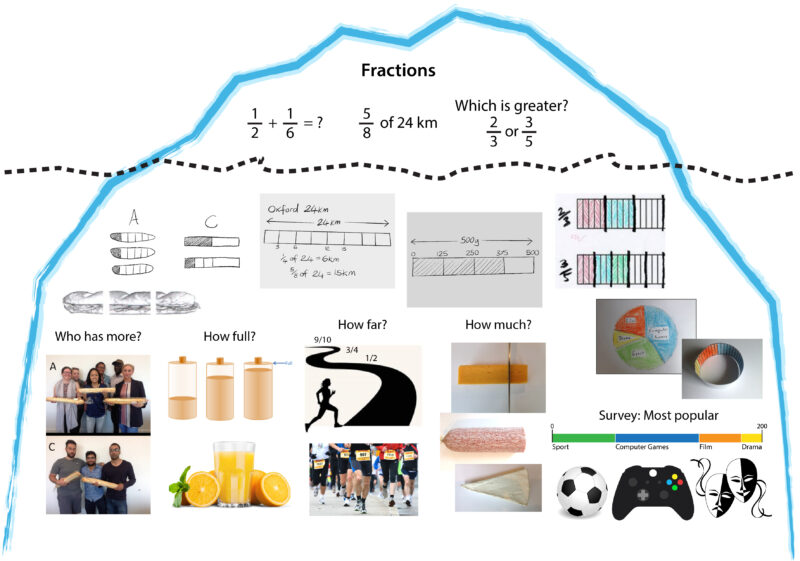
RME materials expose students to multiple contextual situations which can be represented by a ‘model of’ each particular situation. Designers deliberately choose contexts with potential for developing mathematical thinking; for example, asked to depict how to share a subway sandwich, students may begin by making ‘realistic’ drawings, showing round ends and fillings, but in time will move to a rectangular bar ‘model of’ a sandwich with the ends squared off. Producing a drawing to show how to share the sandwich fairly, marking cuts on the rectangular representation and labelling the pieces with fractions, leads to a bar model picture – a fraction bar. Other contexts such as shading in a rectangular cinema layout to represent the number of seats sold would lead to a percentage bar type of bar model. For some contexts such as marking bottle stops on a race route, it may be more appropriate to draw a line showing distance on one side and bottle stop positions on the other. This is sometimes described as a ‘double number line’ but would still be classed as a type of bar model, where the bar has been flattened to look like a line. Overall, models in RME “should ‘behave’ in a natural, self-evident way. They should fit with the students’ informal strategies – as if they could have been invented by them…” (Van den Heuvel-Panhuizen, 2003, p. 14).

The issue of realisable context is a complex one for designers who are concerned about making mathematics truly accessible to all learners, from all communities.   As discussed by Gutstein (2006), there is a tension between teaching for social justice and teaching for mathematical power. This issue is something which we are currently thinking more about with respect to our materials.

Horizontal/vertical mathematisation

In RME, progress is indicated when students start to see the similarities between ‘models of’ situations, and are consequently able to generalise the use of these models and apply them to other problems. At this point they are able to make a shift towards using a bar to represent a situation which is not obviously ‘bar like’, using a bar as a ‘model for’ solving a problem. So progress is defined in terms of formalisation of models (Van den Heuvel-Panhuizen, 2003), and in particular the progression from ‘model of’ to ‘model for’ (Streefland, 1985).  So, for example, students may begin to see how they can use a bar to represent survey data, and to develop connections between segmented bars, pie charts and fractions, ultimately using a bar to compare and add fractions. This shift is also described as vertical mathematisation (Treffers, 1987), where students recognise the mathematical similarity between different problems and are able to choose an appropriate model to solve a problem.  Models, in this view, are far more than given strategies for solving problems; they are central to building the understanding needed to deconstruct a problem.

Guided reinvention

RME pedagogy aims to enable students to connect their informal representations of the world to formal mathematics, building from shared understanding of imaginable contexts to recognition of the mathematical sameness of different problems and the ability to choose an appropriate model to solve a problem (Van den Heuvel-Panhuizen, 2003).  This ‘guided reinvention’ not only requires particular practices on the part of the teacher, it also demands corresponding student modes of participation. These include: social norms of communication (e.g. students listen to others’ contributions, and ask questions when they disagree or do not understand; teacher avoids saying if strategies/solutions are right or wrong); the use of sketches and diagrams (e.g. students represent contexts and strategies with either realistic or more stylised drawings); and teacher modes of response and orchestration (e.g. asking for explanation/agreement, highlighting different student strategies and solutions).

RME classrooms also create a shift in “socio-mathematical norms” (Yackel & Cobb, 1996) – for example, what is an appropriately mathematical statement (e.g. the class agrees on what counts as a mathematically different solution).  RME also brings a shift in who is the authority in the classroom – unlike conventional classrooms, this is no longer the teacher alone; mathematising is a collective effort in which the teacher acts as a guide, orchestrating discussion in which students are able to develop ownership of mathematics. Reflecting the issues raised by Gutstein about context, the tension between the giving up of teacher authority at the same time as the need to guide adds a complexity to RME design and pedagogy.

Read more about RME  techniques for teaching.

For more on our research projects see our past projects pages.

For a list of relevant reading and references, look here.