“Say what you see”
RME design enables students to focus on meaning in mathematics.
Like “What’s the same? What’s different?”, “Say what you see” encourages careful looking to understand how mathematical concepts and representations work. “Say what you see” provides an opportunity to drill down even further into meaning, encouraging students to explore and articulate the relationships within a representation, and generate their own understanding of concepts such as equivalence. It has the added benefits of enabling teachers to gain an insight into students’ thinking, and provides an opportunity for the class to jointly take on and discuss a challenging representation, unpicking it bit by bit.
On this page, we use examples from our materials to show “Say what you see” at work.
Noticing what is there
In Drawing from Data (D2), the whole of Section C is devoted to “Say what you see”. It begins with this rather intriguing depiction of accident data:

This is a very unusual way to depict road safety data. It invites students to look hard at the relationships between the percentages, the placements of the cars, and the speed limits. What can it possibly mean? “Say what you see” invites careful noticing of the arrangement, and speculation about what it is trying to show.

In this next slide, students are invited to make sense of a different representation of accident data. The background is that Sam wants to compare accident rates in his own area (326 in 100 days) with those in a neighbouring area. Can students make sense of the Excel sheet data? Were there only 45 accidents in Faz’s area? “Say what you see” helps them to think about this, to look more closely, and hear more about what other students see.
“Seeing” a mathematical concept
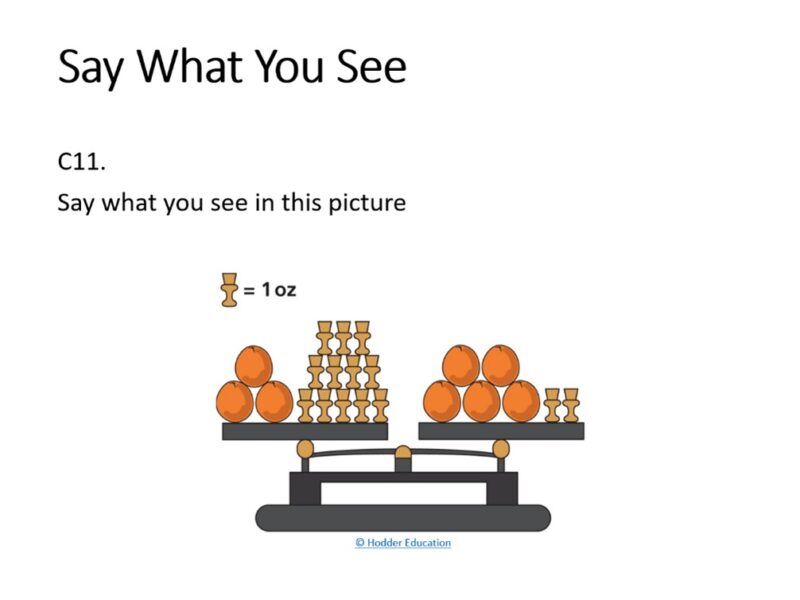
This slide from Knowing the Unknown (A1) invites students to “Say what you see” in the picture, rather than asking them to go directly to working out the weight of one orange. “Say what you see” makes time for observing that there are 3 oranges on the left and 5 on the right, and 12 ounce weights on the left and 2 on the right. Stopping to look in this way helps students to articulate and make sense of their intuitive strategies—like recognising that the scales are in balance so both sides must weigh the same, and then perhaps imagining how removing like-for-like on both sides will keep the balance. In the following slide, where students are invited to look closely at three strategies for working out the weight of an orange, “Say what you see” leads them to gain new insights into the concept of equivalence:
Looking closely at the three different methods and identifying how they work elicits a lot of thinking about how we can know that we are right. The question “Where can you see the weight of an orange?” underlines the need to think hard about what we see. What must be true for Penka’s method to work, and how do we know? Notice how the fact that the scales are in balance is an important part of the seeing, so that talking about equivalence is a natural part of the argument.
Developing tools for thinking
In this video clip, Sue Hough and Jo Kennedy talk about using “Say what you see” as a tool for thinking about the use of the ratio table in Seeing It Differently (N2).
As a general strategy
“Say what you see” works well as a general strategy, even when it isn’t explicitly required in the materials. It contributes to making time for thinking and encourages students to listen and develop their ability to explain their thinking. It enables everyone to have a go – observations can be as simple or as complicated as students want – and it provides a valuable insight for the teacher into how their students are seeing the mathematics, perhaps in ways which are different and interesting. In this video clip, Sue summarises the strategy and talks about its use as a sense-making tool in a GCSE question: