The bar model

In RME, the bar model enables learners to mathematise a range of problems for themselves and make connections within mathematics.

The bar model is probably the best known representation in RME, emerging in a number of forms — fraction bar, percentage bar, double number bar, a double number line — and a wide variety of contexts. What distinguishes our approach to the bar model is that it is not imposed on a particular problem. Instead, it grows out of the chosen context.

In our materials, the bar model makes its first appearance in Fair Sharing (N1), where it is used to compare, simplify and combine fractions. It reappears in Filling the Whole (PR1) where it supports understanding of percentages. In For Every One (PR2), it is applied to sharing in a given ratio and ultimately meets up with the ratio table.

The bar model is an emergent model.

The bar emerges from multiple contexts in our materials. Take this example from Filling the Whole (PR1), where we see the the route from context to bar model representation in this progression of slides:

Students move from talking about what happens when their phone is running out of charge to thinking about the associated battery imagery. This image supports student representations of the battery as a double number bar. Notice in the right-hand slide how the raised top of the battery still appears in this diagram. This is a way of keeping the context alive, even though the bar model is now clearly visible.

The teaching strategy “Say what you see” is used on this slide as a way to help learners focus on these details, making the connections explicit for all members of the classroom. Discussion may arise about whether the phone battery image is actually accurate. This is valuable because, in the mathematised bar model representation, paying attention to scale can be helpful for developing mathematical thinking around fair partitioning.

There are many examples in our materials where contexts are chosen because their associated images are rectangular or striated, like the bar model. Questions associated with these contexts require some form of partitioning. The subway sandwich becomes a fraction bar. The vinaigrette vessel becomes a vertical bar model. The rectangular pizza becomes a double number bar.  Other contexts — sausages, beads, ribbon — all lend themselves to a bar representation. These contexts serve as a foundation from which students can begin to develop their understanding of this mathematical representation.

The bar model is a “model for” more abstract contexts.

Of course, at some stage we want learners to be able to apply a bar model to a situation where the context itself does not necessarily evoke “bar-like” imagery. RME materials are designed so that students naturally generalise from their experience of generating a bar in multiple bar-like contexts, leading them to recognise how to apply the same ideas to other situations. In Section B of Fairing Sharing (N1), students begin to make this move when they are asked to think about water stops on a fun run.

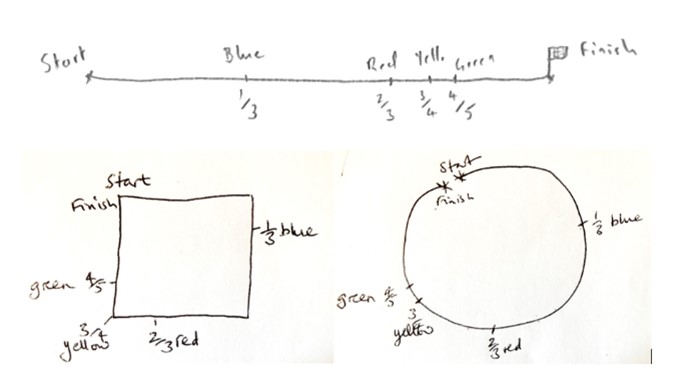
Question B4.b asks learners to draw the route of a 15km run. This should elicit various solutions. Some students may draw a more ‘realistic’ circular or square circuit. But others might realise that that a bar representation makes it easier to think about and work out the answer to question B4.d. Notice that students are asked to be as accurate as possible — this is important at this stage.

Moving further away from obvious bar-like contexts, in Section A of For Every One (PR2), students are shown a way to share £180 in a given ratio by drawing and partitioning a bar model. By saying what they see, learners unpick one possible strategy for finding the value of one of the 12 equal parts of the bar. They are able to represent the £180 on a bar and work with this by drawing on their familiarity with strategies honed from working with bar-like contexts.

The bar model enables students to join up the curriculum.

Like the ratio table, the bar model can be applied to many topics where quantities are related in proportion.